Q1. A microscopic particle of mass 10-26 kg is moving with a kinetic energy of 5 × 10-25 joule. Calculate its de Broglie wavelength.
Solution
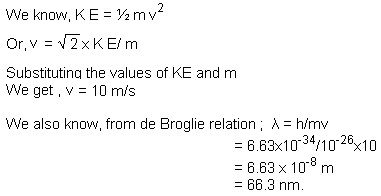
Q2. The shape of the px orbital is:
Solution
All p orbitals are dumb-bell in shape.
Q3. The relationship between de - Broglie wave and momentum of a material particle is -
Solution
The relationship between momentum and wavelength for matter waves is given by  , and the relationship energy and frequency is E = h f. The wavelength
, and the relationship energy and frequency is E = h f. The wavelength  is called the de Broglie wavelength, and the relations
is called the de Broglie wavelength, and the relations  are called the de Broglie relations.
are called the de Broglie relations.
 , and the relationship energy and frequency is E = h f. The wavelength
, and the relationship energy and frequency is E = h f. The wavelength  is called the de Broglie wavelength, and the relations
is called the de Broglie wavelength, and the relations  are called the de Broglie relations.
are called the de Broglie relations.
Q4. Which of the following electronic configurations is impossible?
Solution
The electronic configuration of the third option is not as per the various rules for filling of electrons in various orbitals i.e. Hund's rule of maximum multiplicity, Aufbau principle and Pauli exclusion principle.
Shell Name
Subshell Name
Subshell Max Electrons
K
1s
2
L
2s
2
2p
6
M
3s
2
3p
6
3d
10
N
4s
2
4p
6
4d
10
4f
14
Q5. A sub shell with l = 2 can take up a maximum of:
Solution
Hint: l = 0, 1, 2, 3
Orbitals s p d f
l = 2 corresponds to d orbitals which can take upto 10 electrons.
Q6.
What information does Ψ indicate about wave?
Solution
Ψ gives us the amplitude of wave. It has no physical significance.
Q7. The de Broglie wavelength of a particle is given by
Solution
De-Broglie wavelength is given by 

Q8. Which pair of quantum numbers determine the energy of an electron in an orbital?
Solution
The sum of value of Principal quantum number (n) and Azimuthal quantum number (l) determines the energy of an electron in an orbital.
Q9. Which of the following electronic configurations denote an atom in its ground state?
Solution
This is as per the various rules for filling of electrons in various orbitals i.e. Hund's rule of maximum multiplicity, Aufbau principle and Pauli exclusion principle.
Q10. What is the de Broglie wavelength (m) of a 2.0 kg object moving at a speed of 50 m/s?
Solution
The de Broglie wavelength of an object can be calculated by remembering that 1J = 1 kgm2s-2, which changes h=6.626 x 10-34 kgm2s-1.
From de Broglie relation, using the formula, the wavelength can be calculated as follows:


Q11. Uncertainty in the position of an electron (mass 9.1 x 10-31 kg) moving with a velocity of 300 ms-1, accurate upto 0.001% will be:
Solution
According to Heisenberg's uncertainty principle, the product of uncertainties in position (Δx) and velocity (Δv) ≥  .
Question says, ''accurate up to 0.001%''.
This indicates that the uncertainty in velocity is 0.001% of actual value, 300 m s-1.
.
Question says, ''accurate up to 0.001%''.
This indicates that the uncertainty in velocity is 0.001% of actual value, 300 m s-1.
 Therefore, the uncertainty in position (Δx) can be calculated as follows:
Therefore, the uncertainty in position (Δx) can be calculated as follows:

 .
Question says, ''accurate up to 0.001%''.
This indicates that the uncertainty in velocity is 0.001% of actual value, 300 m s-1.
.
Question says, ''accurate up to 0.001%''.
This indicates that the uncertainty in velocity is 0.001% of actual value, 300 m s-1.
 Therefore, the uncertainty in position (Δx) can be calculated as follows:
Therefore, the uncertainty in position (Δx) can be calculated as follows:

Q12. Which one of the following represents a wrong set of quantum numbers for an electron in an atom? (arranged as n, l, m, and s)
Solution
For n = 3 , values of l cannot be 3; l can have the values from 0 to (n-1).
Q13. A photon has energy of 2.6 eV. What is its wavelength?
Solution
Given, 2.6 e V = 2.6 X 1.6 X 10-19 J = 4.16 X 10-19 J
Now,by using formula,


Q14. What is the energy of a photon that has a wavelength of 12.3 nm?
Solution

Q15. With what energy will the fastest photoelectrons be emitted from a surface whose threshold wavelength is 600 nm, when the surface is illuminated by 400 nm light?
Solution
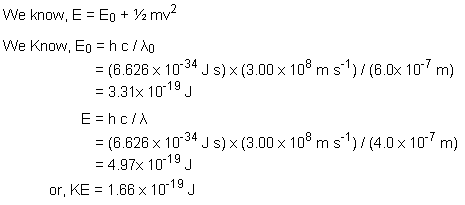
Q16. What is the wavelength of a photon that has energy of 5.25 x 10-19J?
Solution
The wavelength and energy are related by the formula ΔE = hc/λ,
Where h is Planck's constant (= 6.626 x 10-34 Js), c is the speed of light (3.00 x 108 m/s) and λ is the wavelength in meters.
The wavelength can then be calculated by rearranging the above formula as follows:


Q17. The Pauli exclusion principle states that:
Solution
Pauli exclusion principle states that no two electrons in the same atom can have the same set of four quantum numbers identical.
Q18. A radio operator broadcast on the 6-meter band. The frequency of this electromagnetic radiation is __________ MHz.
Solution
The speed of all form of electromagnetic wave is related by the equation c = λ.ν,
Where c is the speed of light = 3.00 x 108 m/s, λ is the wavelength in m and ν is the frequency is s-1 or Hz.
Therefore, ν = 3.0 x108 / 6 = 5 x 108 s-1 = 50 MHz
Q19. Why is the electronic configuration of Cr as [Ar] 4s1 3d5 and not [Ar] 4s2 3d4 as predicted by Aufbau Principle?
Solution
Half filled configurations are more stable.
Symmetry of orbitals leads to stability. Sometimes if we add or remove the electron to make symmetrical distribution of the electrons in the orbital thus the electronic configuration becomes more stable. The Aufbau predicted electronic configuration of Chromium as [Ar] 4s2 3d4 but its actual configuration is [Ar] 4s1 3d5.

Q20. Which of the following electronic configurations is possible?
Solution
According to the various rules for filling of electrons in various orbitals i.e. Hund's rule of maximum multiplicity, Aufbau principle and Pauli exclusion principle; the third option is correct.
Shell Name
Subshell Name
Subshell Max Electrons
K
1s
2
L
2s
2
2p
6
M
3s
2
3p
6
3d
10
N
4s
2
4p
6
4d
10
4f
14
Q21. A magnesium surface has a work function of 3.68 eV. Electromagnetic waves with a 215 nm wavelength strike the surface and eject photoelectrons. Calculate the energy of the photoelectrons in Joules and in electron volts.
Solution
E of 215 nm photon = h c / λ
= (6.626 x 10-34 J s) x (3.00 x 108 m s-1) / (215 x 10-9 m)
= 92.4 x 10-19 J per photon which is equal to 5.77 eV
Hence KE of photoelectrons = 2.09 eV = 3.35 x 10-19 J
Q22. Which of the following radiation has the shortest wavelength.
Solution
x-rays is the correct answer.
The wavelength and frequency are inversely related to each other, thus the radiation with the highest frequency will have the shortest wavelength.
The wavelength may be arranged as, X-ray < ultraviolet < Infra red < microwave.
Q23. Electromagnetic radiation travels through vacuum at a speed of __________ m/s.
Solution
The speed of light (electromagnetic radiation) through vacuum has a constant value of 3.00 x 108 m/s and is independent of the wavelength in vacuum.
Q24. Which set of quantum numbers is correct with n = 3?
Solution
For given n, the possible l values are 0, 1, and 2.
For l =0, possible ml values is 0.
For l =1, possible ml values are: +1,0, -1.
For l =2, possible ml values are: +2,+1,0, -1,-2
There are two possible ms values for each ml value: +1/2 or -1/2
Q25. The de Broglie wavelength of a bullet (mass=7.5g) traveling at 700 m/s is
Solution
The Bohr model says that electrons travel in a circular orbit about the atom and also that the momentum of the electron must have discrete values (quantified).
The de Broglie wavelength equation is:
 Where h is Planck's constant (6.626 x 10-34 J.s) and p is a momentum.
p = mv = mass x velocity = (7.5 x 10-3Kg) x (700m/s) = 5.25 Kg.m/s(Here, mass needs to be in Kg)
Substituting in the above formula, we get,
Where h is Planck's constant (6.626 x 10-34 J.s) and p is a momentum.
p = mv = mass x velocity = (7.5 x 10-3Kg) x (700m/s) = 5.25 Kg.m/s(Here, mass needs to be in Kg)
Substituting in the above formula, we get,

 Where h is Planck's constant (6.626 x 10-34 J.s) and p is a momentum.
p = mv = mass x velocity = (7.5 x 10-3Kg) x (700m/s) = 5.25 Kg.m/s(Here, mass needs to be in Kg)
Substituting in the above formula, we get,
Where h is Planck's constant (6.626 x 10-34 J.s) and p is a momentum.
p = mv = mass x velocity = (7.5 x 10-3Kg) x (700m/s) = 5.25 Kg.m/s(Here, mass needs to be in Kg)
Substituting in the above formula, we get,

Q26. What is the maximum number of electrons that may be present in all the atomic orbitals with principal quantum number 3 and azimuthal quantum number 2?
Solution
The maximum number of electrons that may be present in all the atomic orbitals with principal quantum number 3 and azimuthal quantum number 2 is Ten.
Q27. The smallest particle of an element which can take part in chemical reactions and may or may not exist independently is the
Solution
The basic unit of matter is the atom. It is the smallest particle of an element which can take part in chemical reactions and may or may not exist separately. It consists of sub-atomic particles, i.e., protons, neutrons and electrons.
Q28. How does quantum theory explain the fact that excited potassium atoms emit light at only a relatively few wavelengths?
Solution
Quantum theory only allows for discrete energies to be emitted, not energies at all wavelengths. The discrete energies come from the spacing of the energy levels in which the electrons in potassium move around.
Q29. The nucleus of a tritium atom,  contains
contains
 contains
contains
Solution
Tritium is an isotope of Hydrogen with 1 proton and 2 neutrons.
Q30. Which one of the following statements does apply to atoms which are isotopes of the same element?
Solution
Isotopes are atoms of the same element having same number of protons/electrons but different number of neutrons.
Q31. The energy of a photon in Joules that has a wavelength of 9.0 m is:
Solution

Q32. Use the Aufbau principle to write the ground state electron configuration of the following ions(a) Co3+(b) In3+(c) Bi3-(d) Hg+
Solution
(a) 1s2 2s2 2p6 3s2 3p6 4s2 3d4 (b) 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d8 (c) 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2 4f14 5d10 6p6(d) 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2 4f14 5d9
Q33. Which electronic configuration violate the Pauli's exclusion principle?
Solution
According to Pauli exclusion principle; No two electrons in an atom can have the same set of four quantum numbers.
Q34. Which one of the following represents an impossible arrangement for the values of n, l, ml and ms?
Solution
The possible value of m varies from -l to +l .For example: the possible values of m for l = 2 are -2, -1, 0, +1, +2.
Q35. Anode rays were discovered by
Solution
Goldstein (1900) discovered protons in Anode Ray experiments. Atoms contain positively charged particles called protons. Since atoms contain negatively charged particles, they must contain positively charged particles for them to be electrically neutral.
Q36. The element boron consists of two isotopes, 105B and 115B. Their masses, based on the carbon scale, are 10.01 and 11.01, respectively. The abundance of 105B is 20.0% and the abundance of 115B is 80.0%. What is the atomic mass of boron?
Solution
The percentages of multiple isotopes must add up to 100%. Apply the following equation to the problem: atomic mass = (atomic mass X1) × (% of X1)/100 + (atomic mass X2) × (% of X2)/100 Substituting for boron in this equation: atomic mass of B = 10.01 × 20.0/100 + 11.01 × 80.0/100 atomic mass of B = 2.00 + 8.81 atomic mass of B = 10.81
Q37. Thomson's plum pudding model explained:
Solution
The Thomson's pudding model explained that atoms were spheres of positive charge with electrons embedded in it.
Q38. How are emission, absorption and continuous spectra different?
Solution
Emission spectra are produced by thin gases in which the atoms do not experience many collisions (because of the low density). The emission lines correspond to photons of discrete energies that are emitted when excited atomic states in the gas make transitions back to lower-lying levels.
An absorption spectrum occurs when light passes through a cold, dilute gas and atoms in the gas absorb at characteristic frequencies; since the re-emitted light is unlikely to be emitted in the same direction as the absorbed photon, this gives rise to dark lines (absence of light) in the spectrum.
A continuum spectrum results when the gas pressures are higher. Generally, solids, liquids, or dense gases emit light at all wavelengths when heated.
Q39. Calculate the total no. spectral lines and total spectral lines in Balmer series if electron undergoes a transition from 7th energy level to ground state.
Solution
Total no. of spectral lines = n(n-1)/2
Or, 7(7-1)/2 = 21
Total no. of spectral lines in Balmer series = 7-2 = 5 (this is because for Balmer series n1= 2 and n2 = 3, 4, 5…)
Q40. How does Bohr’s theory account for stability of an atom?
Solution
According to Bohr, as long as an electron remains in a particular permitted circular orbit or stationary state, it neither emits nor absorbs energy. As a result, an electron can not spiral down towards the nucleus loosing energy continuously (as per Maxwell’s theory of electromagnetic radiation). This explains why atoms are stable and do not collapse due to electrostatic attraction between the nucleus and the electrons.
Q41. For radiation which consists of photons of wavelength 4.0 Χ 10-10 m, find: the wave number in cm-1 and the frequency in Hz.
Solution
The wave number is the number of wavelengths in 1 cm.
The wavelength is 4.0 × 10-10 m, so the number of wavelengths in 1 cm = (0.01 m) / (4.0 × 10-10 m)
= 2.5 × 107 cm-1
n = E / h
= (5.0 × 10-16 J)/(6.626 × 10-34 Js)
= 7.5 × 1017 Hz.
Q42. Write electronic configuration of a metal ion which is isoelectronic with Cr3+. What is the number of occupied energy shells, sub shells and Orbitals in it?
Solution
V2+ is isoelectronic with Cr3+ V2+: 1s2, 2s2, 2p6, 3s2, 3p6, 3d3 Hence, Occupied energy shells = 3, Sub shells=6 and Orbitals = 12
Q43. A dust particle of mass 10-11 gm has velocity of 10-4 cm/s. The error in measurement of velocity is 0.1 %. Calculate uncertainty in its position.
Solution
∆V = 0.1 x 10-4/100 = 10-7 cm/s = 10-9 m/s
We know, ∆X. m∆V ≥ h/4π
Hence, ∆V = 6.626 x 10-34/ 4 x 3.14 x 10-14 x 10-9 = 5.27 x 10-12m
Q44. Chlorine has two main isotopes, 35Cl and 37Cl. If the average atomic mass is 35.453, find the abundances of each isotope?
Solution
The abundances of each isotope: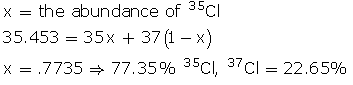
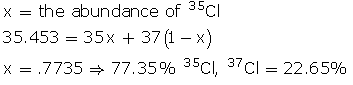
Q45. Account for the fact that manganese has a greater number of oxidation states than zinc even when they have similar electronic configurations.
Solution
Mn is a transition element with an incompletely filled 3d shell. The completely filled 3d shell in zinc leads to stability and removal of the 4s electrons with only a relatively low ionization energy to form the 2+ ion is the only common oxidation state of zinc (+II). The filled 3d orbital cannot participate in bonding. For manganese, both the 3d and 4s sub shells are available for occupation by bonding electrons, so a wide range of oxidation states is observed.
Q46. What is the frequency in Hz of electromagnetic radiation that has a wavelength of 0.53 m?
Solution
The speed of all form of electromagnetic wave is related by the equation c = λ.ν,
Where c is the speed of light (=3.00 x 108 m/s ), λ is the wavelength in m and ν is the frequency is s-1 or Hz.
Therefore, by substituting the values in the formula, we get,
ν = 3.0 x 108 / 0.53
= 5.66 x 108 Hz
Q47. Heating copper (I) chloride to about 1200°C emits blue light having a wavelength of 4.5 x 10-7 m. What amount of energy is emitted by its photons?
Solution
Weknow, E = h Ʋ
Given: λ = 4.5 x 10-7 m
First, find Ʋ using C = λƲ
Ʋ = 3.0 x 108 /4.5 x 10 -7 = 6.6 X 1014 Hz
We know, E = h Ʋ
E = 6.626 X 10-34 X 6.66 X 1014
Hence, E = 4.41 x 10-19 J
Q48.
The intense yellow light from a sodium lamp arises from an electron jump from the 3p to the 3s level. The wavelength of the light is 590 nm (5.9 × 10-7 m). What is the energy for this transition in kJ mol-1?
Solution
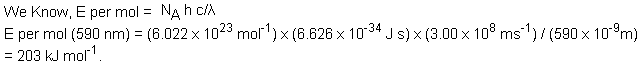
Q49. On the basis of Heisenberg's uncertainty principle, show that the electron can not exist within the nucleus.
Solution
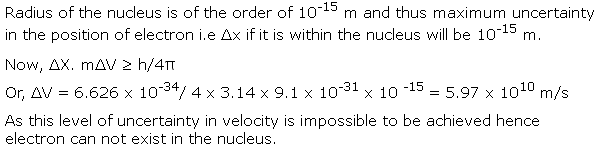
Q50. Describe the Quantum Mechanical Model of the atom.
Solution
The Quantum Mechanical Model is a complex mathematical model. The Quantum Model is based on understanding the behavior of light which is considered to be composed of electromagnetic (EM) waves.
Based on knowing some information about electrons, the location of the electron is predicted. Electrons exit around the nucleus in form of electron clouds called orbitals in different energy levels. Low energy electrons are found near the nucleus; high energy electrons are found further away from the nucleus. Electrons emit energy when fall back in lower energy levels. Energy is released in the form of electromagnetic radiation. When this energy is emitted, it can be observed using special instruments called spectrophotometer. EM spectrum shows all forms of radiation
Q51. Fill in the missing values or names of the following sets of quantum numbers.
n = 2, l = ?, ml = +1; name: 2p
n = ?, l = 0, ml = ?; name: 4s
n = 3, l = 1, ml = +1; name: ?
n = 3, l = ?, ml = 0; name: 3d
Solution
n = 2, l = 1, ml = +1; name: 2p
n = 4, l = 0, ml = 0; name: 4s
n = 3, l = 1, ml = +1; name: 3p
d. n = 3, l = 2, ml = 0; name: 3d
Q52. If the quantum number 'n' has a value of 3, what are the permitted values of the quantum number '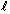 '?
'?
Solution
The permitted values of the quantum number '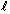 ' are 0, 1, 2.
' are 0, 1, 2.
Q53. Calculate the uncertainty in velocity of a cricket ball of mass 0.15 kg if its uncertainty in position is of the order of 1A0
Solution
We know, ∆X. m∆V ≥ h/4π
Hence, ∆V = 6.626 x 10-34/ 4 x 3.14 x 0.15 x 10 -10 = 3.51 x 10-24 m/s
Q54. What is the wavelength of an electron moving at the same velocity of 1.1 x 103 m s-1? Why is the wave character of matter more apparent with the electron than with the bullet?
Solution

Q55. (i) If the quantum number '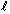 ' has value of 2, what are the permitted values of the quantum number ?(ii) An atomic orbital has n = 3, what are the possible values of
' has value of 2, what are the permitted values of the quantum number ?(ii) An atomic orbital has n = 3, what are the possible values of 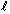 ?(iii) An atomic orbital has
?(iii) An atomic orbital has 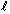 = 3, what are the possible values of
= 3, what are the possible values of 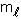 ?
?
Solution
(i) If 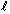 = 2, the permitted values of m are: me = -2, -1, 0, +1, +2(ii) For n = 3,
= 2, the permitted values of m are: me = -2, -1, 0, +1, +2(ii) For n = 3, 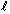 may have the value
may have the value 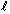 = 0, 1, 2(iii) For
= 0, 1, 2(iii) For 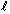 = 3, me may have the values m = -3, -2, -1, 0, +1, +2, +3
= 3, me may have the values m = -3, -2, -1, 0, +1, +2, +3
Q56. How many electrons in a given atom can have the following quantum numbers?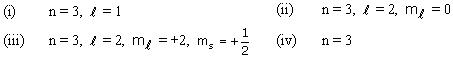
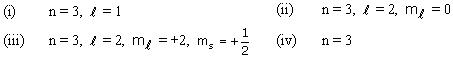
Solution
(i) 6 (ii) 2 (iii) 1 (iv) 18
Q57. What are the values of n, 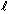 and
and 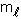 for 3p-orbitals?
for 3p-orbitals?
Solution
For 3p-orbitaln = 4, 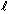 = 1 and
= 1 and 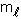 can have any of three values -1, 0, +1.
can have any of three values -1, 0, +1.
Q58. Calculate Ionization energy of He+ if electron is present in 2nd Bohr orbit.
Solution
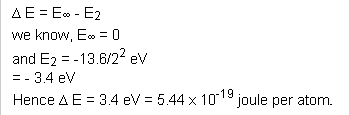
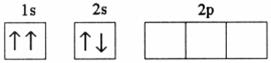
Q59. Of the following electron configurations, state whether each represents an atom in the ground state, a possible excited state, or is incorrect. a) 1s2 2s22p1 b) 1s22s13s1 c) 1s22s22p63s22d2 d) 1s22s42p2 e) 1s12s1
Solution
a) 1s2 2s22p1 - correct
b) 1s22s13s1 -excited
c) 1s22s22p63s22d2 -incorrect
d) 1s22s42p2 -incorrect
e) 1s12s1-excited
Q60. The spectrum of mercury vapor shows strong emission at the wave lengths of 165 nm, 254 nm, 365 nm, 546nm, and 735 nm. Calculate the energy, in kJ mol-1, associated with the lowest wavelength and state in which region of the electromagnetic spectrum it lies.
Solution
The lowest wavelength is 165 nm ( Highest energy carrying photons among the given wavelength)
E per mol = NA h c / λ
E per mol (165 nm)= (6.022 x 1023 mol-1) x (6.626 x 10-34 J s) x (3.00 x 108 ms-1) / (165 x 10-9 m)
= 725 kJ mol-1
This is in the ultraviolet region.
Q61. What are limitations of Bohr’ model?
Solution
According to Bohr’s theory, atom is planer, but now it has been established that atom has 3D existence. Bohr’s model is applicable for single electron system. It fails to explain the line spectra of multi-electron atoms. Each spectral line splits into finer lines when subjected to influence of magnetic field (Known as Zeeman effect) and electric field (known as Stark effect) Bohr’s atomic theory can’t explain this. It was also unable to explain de Broglie’ dual character of matter and Heisenberg’s uncertainty principle.




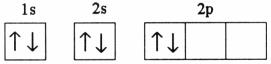
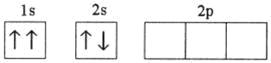 .
.
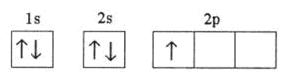 .
.
Comments
Post a Comment